Dimensionality Reduction, Kernel PCA and LDA
Kernel PCA
PCA is a linear method. That is it can only be applied to datasets which are linearly separable.Kernel PCA uses a kernel function to project dataset into a higher dimensional feature space, where it is linearly separable source
Why High Dimension?: VC (Vapnik-Chervonenkis) theory tells us
that often mappings which take us into a
higher dimensional space than the
dimension of the input space provide us
with greater classification power source
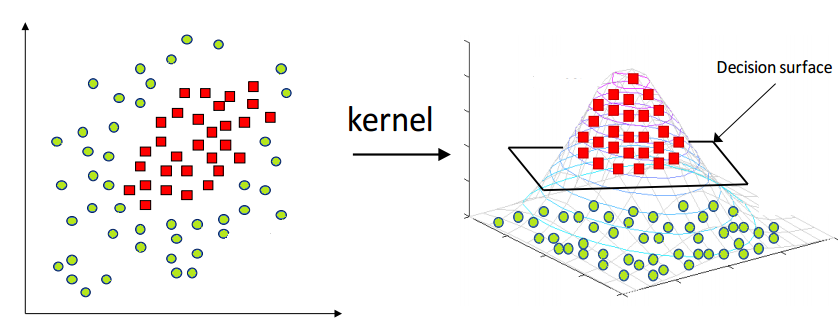
But if we simply map the data into higher dimensions, the computation cost would be also high. Why?:

Here comes the Kernel Trick: Get the benefit of high-dimension, but avoid the computation burden brought by high dimensions.
Given any algorithm that can be expressed solely in terms of dot products, this trick allows us to construct different nonlinear versions of it. And it will save compuational cost. Why?

Popular Kernel funnctions:
Polynomial kernel \(k(x,y)=(x^Ty+1)^d\).
It looks not only at the given features of input samples to determine their similarity, but also combinations of these. With \(n\) original features and \(d\) degrees of polynomial, the polynomial kernel yields \(n^d\) expanded features.
| RBF kernel, also known as Gaussian kernel $$k(x,y)=e^{-\gamma | x-y | ^2}$$. |
There is an infinite number of dimensions in the feature space because it can be expanded by the Taylor Series. The \(\gamma\) parameter defines how much influence a single training example has. The larger it is, the closer other examples must be to be affected
Math: source
Limitation: Overfitting when we mapping features into higher dimensions.
Linear Discriminant Analysis
Main Idea: With tagged data, we can perform supervised dimensionality reduction. The LDA is to project all the data points on to a lower dimension, which seperates the classes as far as possible. source1, source2
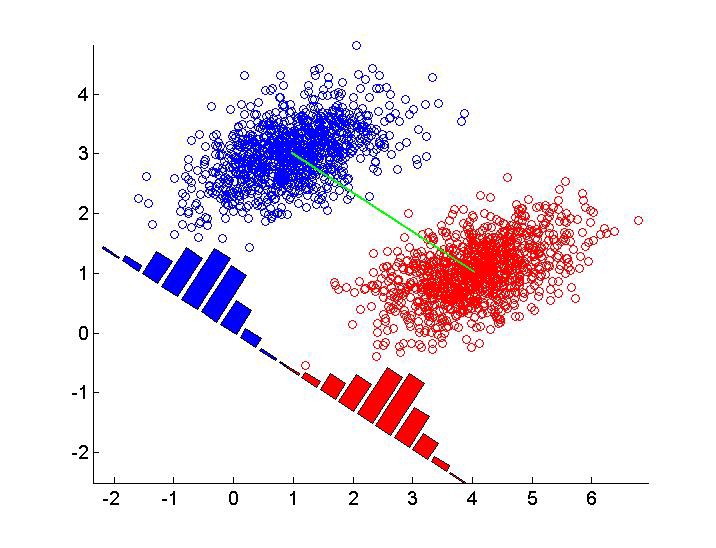
We achieve this by maximizing between-class variance and minimizing within-class variance.
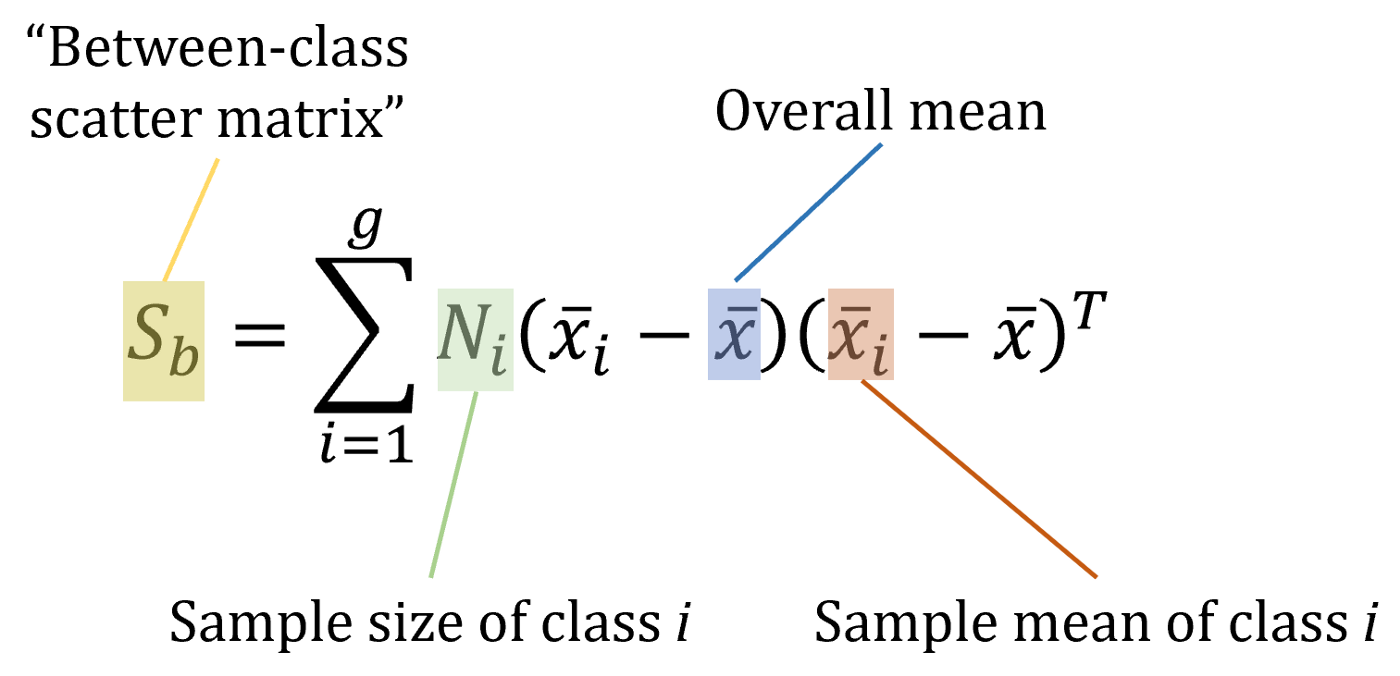
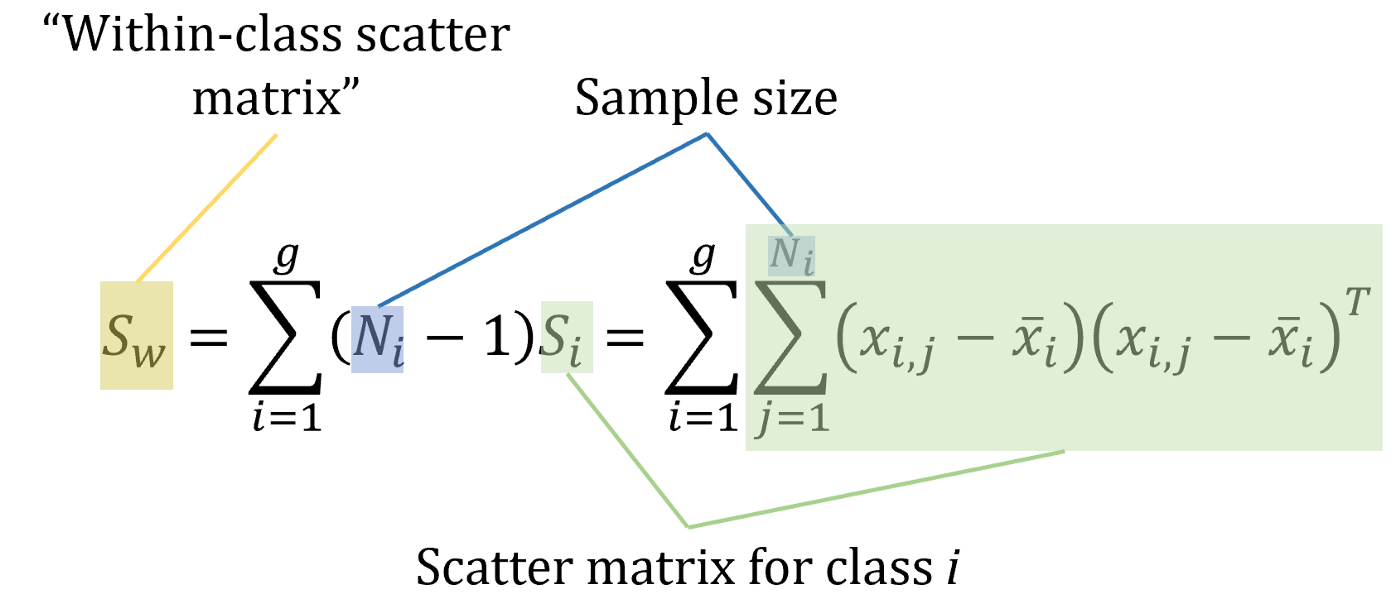
Fisher defined the separation between these two distributions to be the ratio of the variance between the classes to the variance within the classes.
What we can get from LDA?:
Low-dimensional representations of data points, where each class could be largely seperated.

Use Case: Reduce the number of features to a more manageable number before classification
Limitation LDA will fail if discriminatory information is not in the mean but in the variance of the data (That is, the classes share mean value.). We can use Non-linear Discriminant Analysis:source
- Quadratic Discriminant Analysis (QDA): Each class uses its own estimate of variance (or covariance when there are multiple input variables).
- Flexible Discriminant Analysis (FDA): Where non-linear combinations of inputs is used such as splines.
- Regularized Discriminant Analysis (RDA): Introduces regularization into the estimate of the variance (actually covariance), moderating the influence of different variables on LDA.